Today I was talking to a good friend and former colleague and he asked how I would go about laying out a collection of controls as if they were equally spread out around the edge of an ellipse. I did a quick Google and didn’t find much in the way of examples, so I decided to knock one together. An hour later and we have what I present here.

This is a fully working, but a little rough, demonstration of creating your own control and performing custom layout logic.

The Idea

The problem we are trying to solve requires working out the location that a control should be positioned at within its containing panel, such that all of the controls are positioned as if they are placed along the edge of an invisible ellipse.

We can simpify the problem by modelling the edge of the ellipse as a long piece of string that we can straighten out in to a straight line and also assume that each point on the ellipse’s edge is at an angle one unit (degree or radian) greater than the last. This means that the angle to the location of the control around the edge of the ellipse is directly proportional to the distance that the control needs to be from the start of a straight line.

For the control itself I chose to create a new control that inherits System.Windows.Controls.Canvas. The reasoning for this is that Canvas provides everything that we need, meaning we only have to override how items are laid out and a few additional properties to configure the layout.

The Theory

Here we will approach the solution in two steps. The first of which will give us the spacing of the controls, which will allow us to go on and calculate the location of the control.

To calculate how far around the ellipse each control should be placed, we need to know the number of items we want to display and the length of the line we have to display them on. Simple! First, the amount of spacing (space) between each item (where count is the number of items, length is the length of the line) is calculated using:

$ latex space = frac{textsf{length}}{textsf{count}} $

There is one unknown in the above formula: the legth of the line; or more accurately, the circumference of the ellipse. It may come as a suprise to learn that there is no finite equation which will give the circumference of an ellipse. Don’t worry though, we don’t have to get our hands dirty with second degree integrals as some clever chaps have devised equations which will approximate the circumference. 

Several methods exist, each with varying degrees of accuracy. The most accurate of which is the second form of Ramanujan’s approximation (although the accuracy degrades for ellipses where the width is much greater than the height and vice versa) and is given by:

Where:

In code it looks like this:

private double CalculateEllipseCircumferenceRamanujan2(double a, double b)
{
    double h = Math.Pow(a - b, 2) / Math.Pow(a + b, 2);
    //pi (a + b) [ 1 + 3 h / (10 + (4 - 3 h)^1/2 ) ]
    double result = Math.PI * (a + b) * (1 + 3 * h / (10 + Math.Pow((4 - 3 * h), 0.5)));
    return result;
}

Now each control’s distance from the start of the line can be calculated as:

Where ‘index’ is the 0-based index of the control in its parent collection, or some other value which indicates the ordering of elements. It is important to note that by using a 0-based index, our spacing allows space for one extra item which doesn’t actually exist. If we didn’t do this, the last item in the control would be placed on top of the first as they’d both occupy the same position when wrapped around the ellipse.

Given the offset of the control from the start of the line, we need to convert this in to an angle of rotation from the start point of the ellipse’s edge. As stated before, we can assume that each point on the ellipse’s edge directly relates to the distance from the start of the ellipse. So all we need to do is map our value on to a radian number range.

In code:

double theta = (Math.PI * 2) * ((i * itemSpacing) / layoutCirfumference);

We’re almost there! The last step is to now take that angle along with the characterisitcs of the ellipse and calculate a point for a given angle. Thankfully the parametric equations for a point on the edge of an ellipse are nice and simple:

In code:

private Point GetPointOnEllipse(double width, double height, Point origin, double theta)
{
    double x = origin.X + (width * Math.Cos(theta));
    double y = origin.Y + (height * Math.Sin(theta));
    return new Point(x, y);
}

Now if we use the above method for each child control, we will have a collection of evenly spaced points plotting the edge of the ellipse! Woo hoo. Note that when setting the location of a control, you will need to offset these values slightly such that the control is centred on the point, rather than having its top left corner at the point.

The last point of interest in the control’s code is the metadata used to define the characteristics of its dependency properties. Each dependency property registration specifies a FrameworkPropertyMetadata class which makes use of the value FrameworkPropertyMetadataOptions.AffectsArrange. In a nutshell, each time the the value of the property changes, the control’s ArrangeOverride is invoked, updating the layout of any child controls.

public static readonly DependencyProperty EllipseHeightProperty
            = DependencyProperty.Register("EllipseHeight", typeof(double), typeof(EllipticalLayoutPanel),
                                          new FrameworkPropertyMetadata(75d, FrameworkPropertyMetadataOptions.AffectsArrange));

So what’s so great about that? Well it means we don’t have to bother specifying PropertyChangedCallbacks and  then some internal update method, WPF does it for us! If you’re interested in learning more about dependency properties, check out MSDN or for some worked examples, look at my chapter on application development (chapter 1) in ‘WPF Recipes in C# 2008’.

The Solution

Here I present a simple demonstration of the above in the attached solution. The solution contains a simple Window which hosts the custom ellipse layout control. The ellipse layout control is included in the EllipticalLayoutPanel class and adds several dependency properties and a few methods to the Canvas class.

The main window also contains a few controls which allow you to interact with the layout control, allowing you to specify the size and location of the control as well as add or remove items to the control.

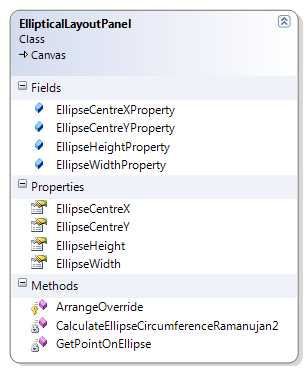
To the right is a class diagram, showing the structure of the layout control. You can see it’s pretty simple and doesn’t need to add much to its Canvas ancestor. The dependency properties are there only for testing as really the dimensions of the ellipse should be automatically calculated using the available size of the control. If there is any desire for this, I could easily extend the solution to perform this, just give me a shout.

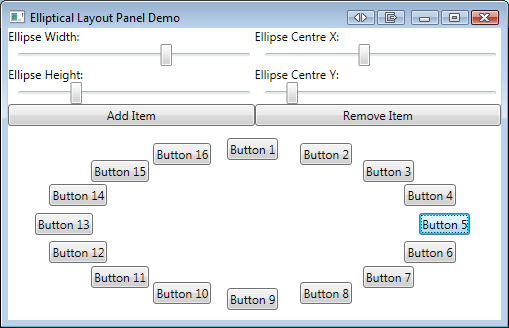
Below is a screenshot of the demo application in action. The values of the sliders are directly bound to the panel’s dependency properties, meaning the only code-behind is for the two button event handlers.

The code is available for download as a Visual Studio 2008 (SP1) solution, built against .Net 3.5 SP1.

All and any comments / bugs / suggestions are welcomed!